Objetivo: El objetivo de este blog es indagar e interactuar en actividades, enlaces y vídeos para cualquier visitante o persona que requiera información sobre: Diferenciales.
4.6 Diferenciales.
Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.
Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.
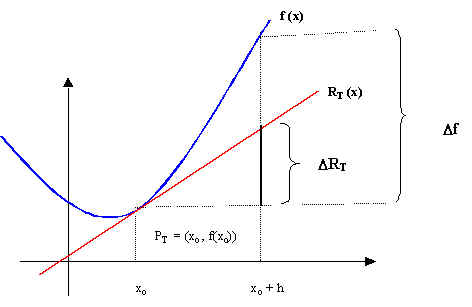
Considerando que la recta tangente es la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia PT, si le llamamos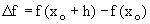
a la variación de f cuando x varía de xo a xo + h y 
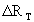a la variación de la recta tangente en el mismo rango de variación en x, podemos afirmar que para valores de h "cercanos" a 0, estas dos variaciones son muy parecidas, es decir, D f @ D RT.
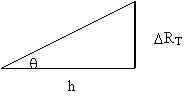
Podemos expresar a D RT en términos de h y el ángulo q que forma la recta tangente con el eje de las abscisas. En el triángulo de la figura, que extraemos a continuación, se observa lo siguiente:
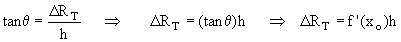En virtud de que D RT es un aproximador de la DIFERENCIA D f, lo definiremos como EL DIFERENCIAL DE f en el punto xo, con respecto al incremento h y lo denotaremos por df, es decir,
DEFINICION Y EJEMPLOS
Consideremos la siguiente ilustración en donde aproximamos a la función f por su recta tangente.
Considerando que la recta tangente es la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia PT, si le llamamos
a la variación de f cuando x varía de xo a xo + h y a la variación de la recta tangente en el mismo rango de variación en x, podemos afirmar que para valores de h "cercanos" a 0, estas dos variaciones son muy parecidas, es decir, D f @ D RT.Podemos expresar a D RT en términos de h y el ángulo q que forma la recta tangente con el eje de las abscisas. En el triángulo de la figura, que extraemos a continuación, se observa lo siguiente:
df = f '(xo)h
Consultado el 27-11-2015 Leer más en:
http://www.mat.uson.mx/eduardo/calculo2/soldifer/soldiferHTML/diferencial.htm
|
ARYA,
J. C. (2009). Matemáticas aplicadas a la administración y la
economía. Ciudad de México: Pearson Educación.
|
No hay comentarios:
Publicar un comentario