3.4 Diferenciabilidad y continuidad.

Objetivo:  El objetivo de este blog es indagar e interactuar en actividades, enlaces y vídeos para cualquier visitante o persona que requiera información sobre: Diferenciabilidad y continuidad.

3.4 Diferenciabilidad y continuidad. Derivada; Diferenciabilidad  La derivada de una función f en el punto a en su dominio se define por f'(a) = lim h0 f(a+h) - f(a) h Decimos que la función f es diferenciable en el punto a en su dominio si f'(a) existe. Diferenciable en un subconjunto del dominio La función f es diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S. Una función puede fallar ser diferenciable en el punto a si lim h0 f(a+h) - f(a) h no existe, o es infinito. En el primer caso, a veces tenemos una cúspide en la gráfica, y en el último caso, obtenemos un punto de tangencia vertical. 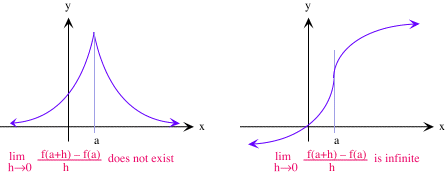Continuidad: La continuidad de una función en un número no implica que la función sea derivable en dicho número; por ejemplo, la función valor absoluto es continua en 0 pero no es diferenciable en cero. Consultado el 27-11-2015 Leer mas en: http://www.zweigmedia.com/MundoReal/calctopic1/contanddiffb.html ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación.