5.2 Extremos relativos y extremos absolutos.

Objetivo: El objetivo de este blog es indagar e interactuar en actividades, enlaces y vídeos para cualquier visitante o persona que requiera información sobre: Extremos relativos y extremos absolutos.

5.2 Extremos relativos y extremos absolutos.

Los extremos relativos se obtienen derivando la función a estudiar e igualando la primera derivada a cero, despejamos la variable,normalmente se llama x, y en caso de que exista solución, esos valores de la x constituyen la coordenada x del punto de los extremos relativos. Lo que no sabemos aún es si son máximos o mínimos, pero son extremos relativos sin ninguna duda. Para poder discernir que tipo de extremos son usaremos el criterio de la segunda derivada.

Los extremos absolutos se calculan usando el “desconocido” Teorema de los valores extremos. Este teorema dice : `Toda función continúa en un intervalo cerrado tiene extremos absolutos (mínimo absoluto y máximo absoluto).´ Es decir, el teorema garantiza la existencia de extremos absolutos para una función continua en un intervalo cerrado pero no dice cómo determinarlos.

EXTREMOS RELATIVOS

Sea , sea  y sea  un punto perteneciente a la función.

Se dice que  es un máximo local de  si existe un entorno reducido de centro , en símbolos , donde para todo elemento  de  se cumple . Para que esta propiedad posea sentido estricto debe cumplirse .

Análogamente se dice que el punto  es un mínimo local de  si existe un entorno reducido de centro , en símbolos , donde para todo elemento  de  se cumple .

EXTREMOS ABSOLUTOS 

Sea , sea  y sea  un punto perteneciente a la función.

Se dice que P es un máximo absoluto de f si, para todo x distinto de  perteneciente al subconjunto A, su imagen es menor o igual que la de . Esto es:

máximo absoluto de 

nálogamente, P es un mínimo absoluto de f si, para todo x distinto de  perteneciente al subconjunto A, su imagen es mayor o igual que la de . Esto es:

 mínimo absoluto de 

Consultado el 27-11-2015 Leer más en:

http://fisicaymates.com/extremos-relativos-y-absolutos-de-una-funcion/

ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación. ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación. Objetivo: El objetivo de este blog es indagar e interactuar en actividades, enlaces y vídeos para cualquier visitante o persona que requiera información sobre: Prueba de la primera derivada para la determinación de máximos y mínimos. 5.3 Prueba de la primera derivada para la determinación de máximos y mínimos. Teorema valor máximo y mínimo "Sea  un punto crítico de una función  que es continua en un intervalo abierto  que contiene a . Si  es derivable en  el intervalo, excepto posiblemente en , entonces  puede  clasificarse como sigue." 1. Si  ' cambia de positiva a negativa en , entonces  tiene un máximo relativo en . 2. Si  ' cambia de negativa a positiva en , entonces  tiene un mínimo relativo en . 3. Si  ' es positiva en ambos lados de  o negativa en ambos lados de c, entonces  no es ni un mínimo ni un máximo relativo.  Criterio de la primera derivada La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos: 1.- Cuando la derivada es positiva la función crece. 2.- Cuando la derivada es negativa la función decrece. 3.- Cuando la derivada es cero la función tiene un máximo o un mínimo. Sea f(x) una función y c un número en su dominio. Supongamos que existe a y b  con a<c<b tales que 1.-  f es continua en el intervalo abierto (a,b) (de acuerdo con el teorema de Rolle) 2.- f es derivable en el intervalo abierto (a,b), excepto quizá en c; 3.- f´(x) es positiva para todo x<c en el intervalo y negativa para todo x>c en el intervalo. Entonces f tiene un máximo local en c. Nótese que un criterio similar puede tenerse para obtener un mínimo local, solo es necesario intercambiar  “positivo”  por “negativo”.   De manera intuitiva podemos observar que para determinar si existe un máximo o un mínimo  basta graficar alrededor de los puntos donde se ha presentado un cambio de signo Es también importante tener en consideración que el termino alrededor del cambio de signo de la derivada de la función es muy relativo y es este punto donde tenemos que tener la máxima consideración. Un punto mas a considerar es el tener en cuenta que solo es necesario considerar no solo el cambio de signos para la derivada Por ejemplo, para el caso de la función: la función entre el intervalo (-1,1) tiene un cambio de signo, sin embargo, la función no es diferenciable en el punto x = 0, pese a eso si existe un mínimo local. Consultado el 27-11-2015 Leer más en: https://es.wikipedia.org/wiki/Criterio_de_la_primera_derivada http://dieumsnh.qfb.umich.mx/DIFERENCIAL/criterio_de_la_primera_derivada.htm ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación. El objetivo: De este blog es indagar e interactuar en actividades, enlaces y vídeos para cualquier visitante o persona que requiera información sobre: Concavidad, puntos de inflexión y prueba de la segunda derivada. 5.4 Concavidad, puntos de inflexión y prueba de la segunda derivada. DEFINICIÓN El punto que, en una función continua, separa la parte convexa de la cóncava, se llama punto de inflexión de la función. En ellos la función no es cóncava ni convexa sino que hay cambio de concavidad a convexidad o al revés. Los puntos de inflexión están caracterizados por:  TEOREMA  Sea  la ecuación de una función. Si  no existe, y la derivada  cambia de signo al pasar por el valor de x=a, entonces, el punto de la función de abscisa x=a es un punto de inflexión. Clasificación de los puntos de inflexión  El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos. Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a , y  debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y  debe ser un máximo relativo de . Teorema Sea  una función tal que  y la segunda derivada de  existe en un intervalo abierto que contiene a  1.  Si , entonces  tiene un máximo relativo en . 2.  Si , entonces  tiene un mínimo relativo en . 1.  Si , entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en , un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada. Consultado el 27-11-2015 Leer más en: http://thales.cica.es/rd/Recursos/rd99/ed99-0295-01/punto7/punto7.html https://es.wikipedia.org/wiki/Criterio_de_la_segunda_derivada    ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación. 5.5 Optimizaciòn de funciones econòmico-administrativas: Maximizaciòn de funciones de ingreso, utilidad y beneficios; minimizaciòn de funciones de costos y costos promedio. MÁXIMOS Y MÍNIMOS 1. (UTILIDAD MAXIMA) Una empresa vende todas las unidades producidas a $4.00 cada una. El gasto total de la empresa G por producir x unidades esta dado en dólares por  G=50+1.3x+0.001x² a) Escriba la expresión para la utilidad total P como una función x. b) Determine el volumen de producción x de modo que la utilidad P sea máxima. c) ¿Cuál es el valor de la utilidad máxima? P=4 C=50+1.3x+0.001x² A) P=4x-50-1.3x-0.001x²≠ P=2.7x-50-0.001x² P'(x)=0.002x-2.7 2.7 0.002 =x B) x=1350≠ P=2.7 (1350)-0.001(1350)2 -50 C) P=1,772.50 ≠ 2. (Costo promedio mínimo) El costo promedio de fabricar cierto artículo es  C=5+48x+3x2  En donde x es el número de artículos producidos. Encuentre el valor mínimo de C. C=5+48x+3x2 C=5+48x-1+3x2 C'=48x2+6x O=6x- 48x2 6x(x2)=48 x3= 486 X=2 ≠ C=5+482+3(2)2 C=5+482+3(4) C=41≠ C es 41 cuando x=2 3. (Costo promedio mínimo) El costo de producir x artículos de cierto producto es: C (x) =4000+3x+10-3x2 Determine el valor de x que hace del costo promedio por artículo un mínimo. C(x)=4000+3x+0.001x2  Cx=4000x+ 3xx+ 0.001x2x C(x)=4000x-1+3+0.001x C'x=-4000x-2+0.001 C'(x)=-4000x2+0.001 -4000x2+0.001=0 -0.001(x2)=4000 0.001(x2)=4000 x= 210000.001 x= 2000 4. (Utilidad máxima) En el ejercicio anterior, los artículos en cuestión se venden a $8.00 cada uno. Encuentre el valor de x que maximiza la utilidad y calcule la utilidad máxima. C(x)=4000+3x+0.001x2  I=8x G=8x - 4000-3x - 0.001x2  G=5x – 4000 - 0.001x2  G'=5 - 0.002x 50.002=x X=2500 G=5(2500) – 4000 – 0.001 (2500)2 =12500 – 4000 – 6250 G=2250 Consultado el 27-11-2015 Leer más en: http://alejandragomezmorales.blogspot.mx/2015/05/55-optimizacion-de-funciones-economico.html    ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación. 5.6 Elasticidad: elasticidad de la demanda y elasticidad del ingreso. 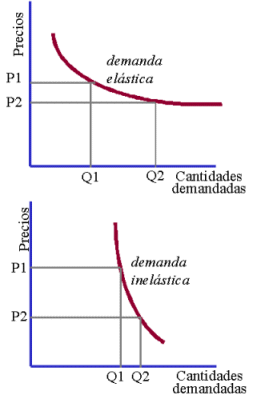La elasticidad de la demanda se mide calculando el porcentaje en que varía la cantidad demandada de un bien cuando su precio varía en un uno por ciento. Si el resultado de la operación es mayor que uno, la demanda de ese bien es elástica; si el resultado está entre cero y uno, su demanda es inelástica. Los factores que influyen en que la demanda de un bien sea más o menos elástica son: 1) Tipo de necesidades que satisface el bien. Si el bien es de primera necesidad la demanda es inelástica, se adquiere sea cual sea el precio; en cambio si el bien es de lujo la demanda será elástica ya que si el precio aumenta un poco muchos consumidores podrán prescindir de él. 2) Existencia de bienes sustitutivos. Si existen buenos sustitutos la demanda del bien será muy elástica. Por ejemplo, un pequeño aumento en el precio del aceite de oliva puede provocar que un gran número de amas de casa se decida por usar el de girasol. 3) Importancia del bien en términos de coste. Si el gasto en ese bien supone un porcentaje muy pequeño de la renta de los individuos, su demanda será inelástica. Por ejemplo, el lápiz. Las variaciones en su precio influyen muy poco en las decisiones de los consumidores que desean adquirirlos. 4) El paso del tiempo. Para casi todos los bienes, cuanto mayor sea el período de tiempo considerado mayor será la elasticidad de la demanda. Puede ser que al aumentar el precio de la gasolina, su consumo no varíe mucho, pero al pasar el tiempo podrá ser substituida en algunos de sus usos por el carbón, en otros usos por el alcohol, de forma que la disminución en la demanda sólo se nota cuando pasa el tiempo. 5) El precio. finalmente hay que tener en cuenta que la elasticidad de la demanda no es la misma a lo largo de toda la curva. Es posible que para precios altos la demanda sea menos elástica que cuando los precios son más bajos o al revés, dependiendo del producto de que se trate. ELASTICIDAD INGRESO DE LA DEMANDA La elasticidad ingreso de la demanda , llamada a veces elasticidad demanda-renta, mide cómo afectan las variaciones de la renta o ingresos de los consumidores a la cantidad demandada de un bien. El coeficiente de elasticidad ingreso de la demanda e I se calcula dividiendo la variación porcentual de la demanda por la variación porcentual de la renta. 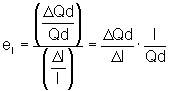De acuerdo al valor de e I , los bienes se pueden clasificar como: •  Bienes normales: Son aquellos cuyo coeficiente de elasticidad ingreso es positivo. Esto significa que cuando aumentan los ingresos del consumidor, la demanda de los bienes normales también aumenta. Pueden ser: •  Bienes de lujo: Su coeficiente de elasticidad ingreso es mayor que 1. Es decir, cuando los ingresos del consumidor aumentan, la demanda crece en una proporción mayor. •  Bienes básicos: Su coeficiente de elasticidad ingreso es positivo y menor que 1. Es decir, cuando los ingresos del consumidor aumentan, la demanda crece en una proporción menor. •  Bienes inferiores: Su coeficiente de elasticidad ingreso es negativo. Por tanto, cuando los ingresos del consumidor aumentan, la demanda de estos bienes disminuye porque el consumidor puede optar por otros productos de mayor calidad. 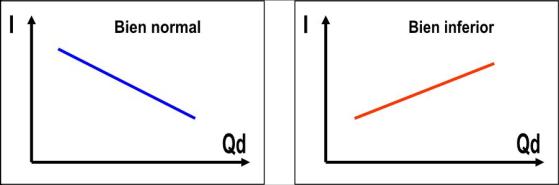Debido a la variabilidad de la elasticidad ingreso, un bien puede ser de lujo a niveles bajos de ingreso y un bien inferior a niveles altos de ingreso. ELASTICIDAD CRUZADA DE LA DEMANDA La elasticidad cruzada de la demanda mide cómo evoluciona y se modifica la demanda de un bien cuando cambia el precio de otro. La elasticidad cruzada se calcula dividiendo el cambio porcentual de la cantidad demandada del bien X ante una variación porcentual del precio del bienY . Si los bienes son sustitutivos (por ejemplo, distintas marcas de automóviles) el aumento del precio de la marca X puede aumentar las ventas de la marca Y , por lo que la elasticidad cruzada será positiva. Si los bienes son complementarios, por ejemplo, los ordenadores o computadoras y el software, el aumento del precio de uno disminuirá las ventas del otro, por lo que la elasticidad cruzada será negativa. Si los bienes son independientes, por ejemplo, teléfonos y cepillos de dientes, por mucho que aumente el precio de uno no variará la demanda del otro, por lo que la elasticidad cruzada será cero. 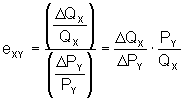El coeficiente de elasticidad cruzada del bien X con respecto al bien Y se define como: ELASTICIDAD PRECIO DE LA OFERTA La elasticidad precio de la oferta mide cómo la variación del precio de un bien afecta a la cantidad ofrecida de ese bien, cuando todos los demás factores permanecen constantes. Se calcula dividiendo el cambio porcentual en la cantidad ofrecida por el cambio porcentual del precio. El coeficiente de la elasticidad precio de la oferta ( e O ) es una medida del cambio porcentual de la cantidad ofrecida de un artículo por unidad de tiempo, que resulta de una variación porcentual del precio del artículo. 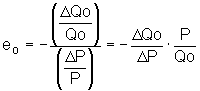Si ?Qo representa el cambio en la cantidad ofrecida de un artículo debido a un cambio en su precio ?P, el coeficiente de elasticidad se define como: De acuerdo a este criterio, la oferta se puede clasificar en elástica (si e O > 1), inelástica (si e O < 1) y unitaria (si e O = 1). Se pueden encontrar e O arco y e O punto de la misma forma que e arco y e punto. Consultado el 27-11-2015 Leer más en: http://www.eumed.net/cursecon/4/elasticidad-demanda.htm http://www.aulafacil.com/cursosenviados/cursomicroeconomia/Lecc-7.htm    ARYA, J. C. (2009). Matemáticas aplicadas a la administración  y la economía. Ciudad de México: Pearson Educación.